This paper deals with the primary factors and countermeasures to prevent falls in seniors in an aging society. Falls among seniors are emerging as a serious social and economic problem, leading to psychological trauma, physical injuries, long-term disabilities, fatalities, and increased medical costs. Therefore, fall prevention is essential for improving an individual’s quality of life and reducing social costs. This study aims to analyze the key physical factors contributing to elderly falls and propose practical strategies for their prevention. To achieve this objective, the study addresses the following research questions: First, what are the differences in impact forces between linear and rotational motion during falls? Second, how can the relationship between impact duration and impulse be quantitatively assessed in relation to actual injury risk? To answer these questions, a physical analysis was conducted by categorizing seniors’ fall types into linear and rotational falls, utilizing linear and angular momentum principles and impact force calculations. The impact force was determined using the law of energy conservation and momentum change, and a simulation was performed using Pygame to validate the theoretical findings. Based on the results, this paper aims to contribute to developing effective fall prevention measures and establish a stronger social foundation to ensure a safer and healthier aging society.

1. Introduction

The aging population is rapidly increasing worldwide, especially in advanced countries like South Korea [1]. As advancements in medical technology and improving living standards increase the average life expectancy, the proportion of seniors is also sharply rising [2]. This brings about significant social and economic issues, among which falls have emerged as a major problem affecting seniors’ health and quality of life [3]. Senior falls are not just a matter of physical injury but also act as psychological trauma [4]. In severe cases, they can lead to long-term disability or death, increasing medical costs and necessitating long-term care, thereby imposing social burdens.[5] These accidents negatively impact seniors’ physical and mental health, making independent living difficult and potentially deepening social isolation [6].

In other words, senior falls not only degrade the quality of life of individuals but also exacerbate the economic bur- den on society [7]. Therefore, preventing these accidents is crucial to improving the quality of life of individuals and reducing social costs and building a safer and healthier aging society [8]. This article starts from this awareness and seeks to explore practical measures to prevent falls in the era of aging [9].

In summary, this article aims to contribute to the promotion of senior health and the creation of a safe living environment by analyzing the main causes and risk factors for falls and presenting prevention strategies based on these analyses [10]. Furthermore, it will derive practical and applicable prevention measures through the opinions of various experts and case studies [11]. Finally, the objective is to help establish a social foundation where seniors can enjoy a healthier and happier old age [12].

The journal highlights the increasing frequency of drop attacks with advancing age. For instance, a study reported that the incidence of drop attacks among people 65 years and older rose from 2 percent in the 65-74 age group to 15 percent in those aged 90 and above [13]. Also, surveys of people living at home have revealed that one third of all seniors experience at least one fall yearly. Approximately four percent of individuals aged 65 and older seek medical treatment for fall-related injuries at least once each year [14].

The impact force is a large contact force between objects upon impact or collision. Force is a physical quantity observed when a mass-bearing object moves with a certain acceleration. It can be described as a temporal change in momentum. Momentum can be calculated by multiplying mass and velocity. In other words, impact force becomes more significant as the moving object’s mass increases and the change in velocity, or acceleration, increases.

Next, Impulse refers to the change in momentum within a specific time frame. The unit of impulse quantity is the same as that of momentum. Additionally, the impulse can be calculated by multiplying the force by time, that is, by multiplying the impact force by the collision time.

2. Method

In this study, air resistance was neglected and free-fall motion was assumed. Furthermore, the elastic effects of the impact surface were not considered.

Energy conservation law :

$$mgh = \frac{1}{2}mv^{2}\tag{1}$$

Impulse-momentum relationship :

$$p = \Delta mv = \Delta m \sqrt{2gh}\tag{2}$$

Impact force calculation :

$$I = \frac{m\sqrt{2gh}}{t}\tag{3}$$

2.1. The Reason for the Theory to Emerge

The first formula used to analyze the fall of a senior is derived from the law of conservation of mechanical energy:

$$mgh = \frac{1}{2}mv^{2}\tag{4}$$

This equation states that if there is no friction or air resistance and an object is dropped, the potential energy of the object is transformed into kinetic energy. Simplifying Equation 4 for velocity, we obtain:

$$p = m\sqrt{2gh} \tag{5}$$

Next, to calculate the impact force experienced by a senior during a fall, we use the momentum formula:

$$p = mv = \Delta mv = \Delta m\sqrt{2gh} \tag{6}$$

The impact force is the product of the change in momentum and collision time. Since the velocity is \(\sqrt{2gh}\), the change in momentum Δ𝑚𝑣 becomes:

$$\Delta mv = \Delta m\sqrt{2gh} \tag{7}$$

Finally, the impact force can be calculated using the equation:

$$I = \frac{m\sqrt{2gh}}{t} \tag{8}$$

Using a mathematical binomial from Equation 7, the force that the object receives is calculated by dividing the impact force by the collision time. Since the impact force represents the change in momentum, it can also be defined as the difference in momentum divided by the collision time. From Equation 5, the force becomes Equation 8.

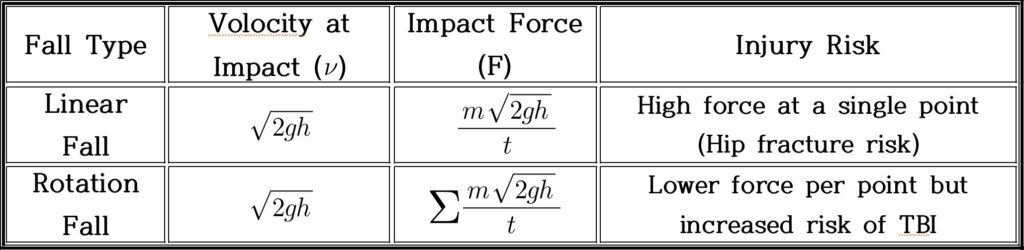
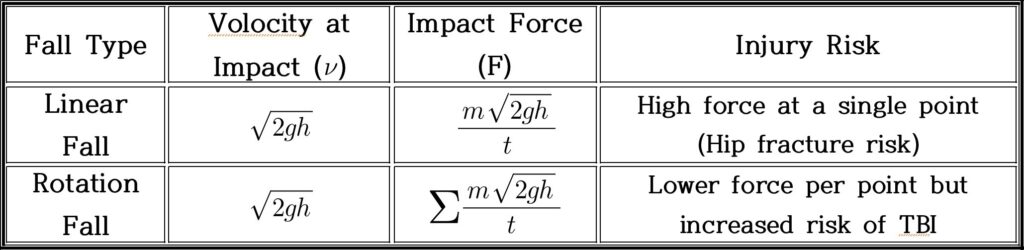
Figure 1 (a), which is on the left, represents a scenario in which a senior individual falls while rotating, which can happen in environments such as a wet restroom where slipping can induce rotational motion. In this case, the individual’s body experiences angular motion as it rotates while falling. The analysis of this fall considers the torque generated during the spin, which plays a crucial role in determining the impact force upon impact. The torque is calculated on the basis of the body’s rotational inertia and the angular acceleration during the fall. This type of fall involves analyzing both linear and angular momentum to accurately assess the force exerted on the body at the point of contact with the ground. (b), which is on the right, represents a senior individual falling linearly, often due to loss of leg strength or balance, resulting in a direct collapse. In this scenario, the person falls straight down without rotational movement. To calculate the impact force, we apply the principle of mechanical energy conservation. The potential energy before the fall (due to the individual’s height above the ground) is converted into kinetic energy as the person descends. The impact force is determined by the rate of deceleration upon contact with the ground, which is influenced by factors such as the person’s height, body mass, and the surface’s ability to absorb shock.

2.2. Torque

Torque, also known as the moment of force, refers to the rotational force applied to an object about a pivot or axis. Mathematically, the torque (𝜏) is calculated as follows:

\(\tau = rF\sin(\theta)\)

where, 𝑟 is the distance from the pivot point (the axis of rotation) to the point where the force is applied. 𝐹 is the amount of force applied. 𝜃 is the angle between the force and the lever arm.

When a person falls, especially in cases involving slipping or tripping, rotational forces (torques) often come into play. Torque influences the body’s movement because the forces acting on different body parts (like the feet losing traction or a sudden push) create rotation about the body’s center of mass. Here is why torque matters:

First, in rotational motion, if a person slips in a way that causes the upper body to rotate (e.g., losing balance backward or forward), the torque determines how fast the body rotates. This rotation can lead to specific impact points (e.g., head, hip, or hands), depending on how the torque influences the fall trajectory.

Second, for the impact force distribution. During a fall, the rotational motion caused by the torque may direct the impact toward specific areas like the hip or shoulder. Understanding this helps predict injury patterns (e.g., rotational falls leading to hip fractures).

Third, for balance recovery, the torque plays a role in restoring balance. For instance, minor adjustments in body movement (e.g., swinging arms or stepping forward) generate counteracting torques that can help a person stabilize and prevent a fall.

Fourth, the surface on which the person slips (for example, wet or uneven floors) can amplify the torque by increasing rotational acceleration, making falls more severe.

In research, analyzing the torque during falls allows for a better understanding of the mechanics of the accident. This knowledge is used to design interventions such as assistive devices, protective gear, or training to reduce the risk of severe injuries. In summary, torque is crucial in the dynamics of falls because it dictates how the body rotates and impacts the ground, influencing the severity of injury and recovery mechanisms. Understanding torque can help create safer environments and preventive measures for individuals, particularly seniors.

2.3. Impact Force Analysis in Linear and Rotational Falls

To analyze the forces exerted during a fall, we apply fundamental physics principles, including the law of energy conservation, the impulse-momentum theorem, and the torque equation.

2.3.1. Linear Fall: Concentrated Impact at a Single Point

In a linear fall, applying the impulse-momentum relationship, the impact force is expressed as:

$$I = \frac{m\sqrt{2gh}}{t} \tag{9}$$

Here, 𝑡 represents the duration of the collision. Since 𝑡 is typically very short in direct falls, the force is highly concentrated at a single point, leading to a high peak force per unit area and increasing the likelihood of fractures, particularly
in the hip region. This highlights the importance of prolonging impact duration (e.g., by shock-absorbing flooring or protective padding) to mitigate the severity of injury (see Figure 2).

2.3.2. Rotational Fall: Distributed Impact Across Multiple Points

In a rotational fall, the body’s center of mass follows a similar downward trajectory with the same velocity at impact:

$$v = \sqrt{2gh} \tag{10}$$

However, due to the presence of angular motion, multiple body segments may contact the ground at different times. The torque equation governs this rotational motion:

$$\tau = r \cdot F \cdot \sin(\theta) \tag{11}$$

Here, 𝜏 represents the torque, describing the rotational effect of a force applied at a distance from a pivot point. 𝑟 is the perpendicular distance from the pivot point (e.g., feet or hip) to the line of action of the applied force. Lastly, 𝜃 represents the angle between the applied force and the lever arm, determining the effectiveness of the force in generating rotation.

Since impact is distributed over multiple points, the force experienced at each contact point is given by:

$$I_i = \frac{m_i\sqrt{2gh}}{t_i} \tag{12}$$

Here, 𝑚_𝑖 represents the mass distribution at each contact point, influencing how the impact force is absorbed across different regions of the body. Similarly, 𝑡_𝑖 denotes the impact duration at that specific location, affecting the magnitude of force experienced at each point. Because multiple regions of the body absorb the force over slightly different time frames, no single point experiences the full force of impact, reducing the risk of fractures but increasing the likelihood of traumatic brain injuries (TBI) or skull fractures if the head is involved (see Figure 3).

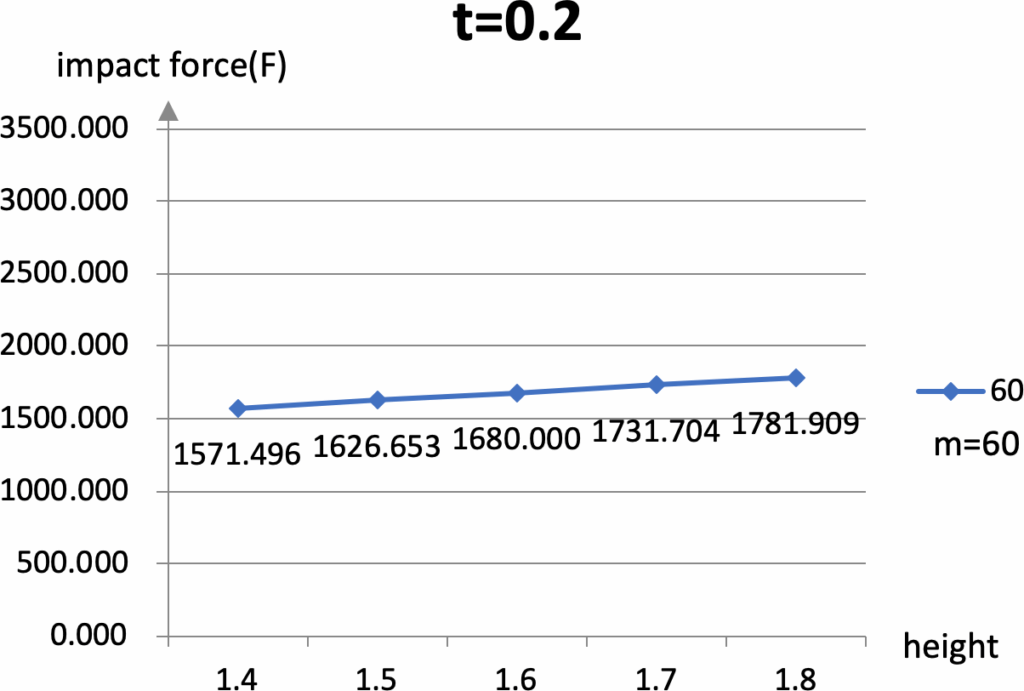
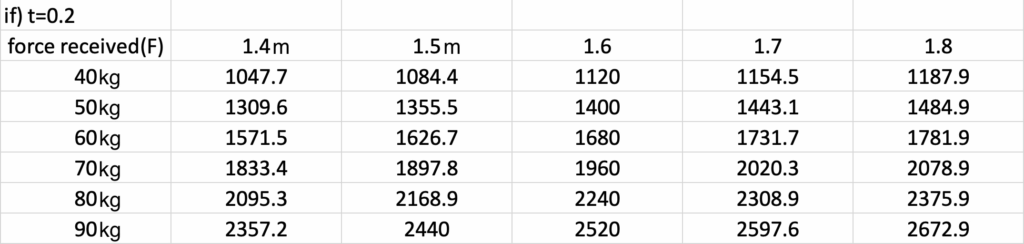
2.4. Comparison of Impact Forces

The comparison of impact forces between linear and rotational falls is shown in Figure 5. While the total impulse remains unchanged, the distribution of force differs, directly influencing injury patterns.

2.5. Code

import pygame
import sys
import numpy as np
import imageio

pygame.init()

WIDTH, HEIGHT = 800, 600 screen = 𝑝𝑦𝑔𝑎𝑚𝑒.𝑑𝑖𝑠𝑝𝑙𝑎𝑦.𝑠𝑒𝑡_{𝑚𝑜𝑑𝑒}((WIDTH, HEIGHT)) 𝑝𝑦𝑔𝑎𝑚𝑒.𝑑𝑖𝑠𝑝𝑙𝑎𝑦.𝑠𝑒𝑡_{𝑐𝑎𝑝𝑡𝑖𝑜𝑛}(“Senior Fall Simulation – Human Model”)

WHITE = (255, 255, 255)
BLACK = (0, 0, 0)
RED = (255, 0, 0)
BLUE = (0, 0, 255)

gravity = 9.8 (𝑚/𝑠²)
scale = 50
𝑓𝑎𝑙𝑙_{𝑠𝑝𝑒𝑒𝑑} = 0
𝑓𝑎𝑙𝑙_{𝑡𝑖𝑚𝑒} = 0
𝑑𝑒𝑙𝑡𝑎_𝑡 = 0.05

𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ}, 𝑐ℎ𝑎𝑟_{ℎ𝑒𝑖𝑔ℎ𝑡} = 40, 80
𝑐ℎ𝑎𝑟_𝑥 = WIDTH // 2
𝑐ℎ𝑎𝑟_𝑦 = HEIGHT // 4
angle = 0
𝑟𝑜𝑡𝑎𝑡𝑖𝑜𝑛𝑎𝑙_{𝑓𝑎𝑙𝑙} = True

𝑓 𝑙𝑜𝑜𝑟_𝑦 = HEIGHT – 50

clock = pygame.time.Clock()

frames = []
running = True
while running:
screen.fill(WHITE)
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False

𝑓𝑎𝑙𝑙_{𝑠𝑝𝑒𝑒𝑑} += gravity * 𝑑𝑒𝑙𝑡𝑎_𝑡 * scale
𝑓𝑎𝑙𝑙_{𝑡𝑖𝑚𝑒} += 𝑑𝑒𝑙𝑡𝑎_𝑡
𝑐ℎ𝑎𝑟_𝑦 += 𝑓𝑎𝑙𝑙_{𝑠𝑝𝑒𝑒𝑑} * 𝑑𝑒𝑙𝑡𝑎_𝑡

if 𝑟𝑜𝑡𝑎𝑡𝑖𝑜𝑛𝑎𝑙_{𝑓𝑎𝑙𝑙} :
angle += 5

if 𝑐ℎ𝑎𝑟_𝑦 + 𝑐ℎ𝑎𝑟_{ℎ𝑒𝑖𝑔ℎ𝑡} >= 𝑓𝑙𝑜𝑜𝑟𝑦:
𝑐ℎ𝑎𝑟_𝑦 = 𝑓𝑙𝑜𝑜𝑟𝑦 – 𝑐ℎ𝑎𝑟_{ℎ𝑒𝑖𝑔ℎ𝑡}
𝑓𝑎𝑙𝑙_{𝑠𝑝𝑒𝑒𝑑} = 0
𝑟𝑜𝑡𝑎𝑡𝑖𝑜𝑛𝑎𝑙_{𝑓𝑎𝑙𝑙} = False

𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} = pygame.Surface((𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ}, 𝑐ℎ𝑎𝑟_{ℎ𝑒𝑖𝑔ℎ𝑡}),pygame.SRCALPHA) 𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒. 𝑓𝑖𝑙𝑙}((0, 0, 0, 0))

pygame.draw.circle(𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} , BLUE, (𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 2, 15), 15)

pygame.draw.rect(𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} , RED, (𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 4, 30, 𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 2, 40))

pygame.draw.line(𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} , BLACK, (𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} //2, 70), (𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 4, 90), 4) pygame.draw.line(𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} , BLACK, (𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 2, 70), (3 * 𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 4, 90), 4)

pygame.draw.line(𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} , BLACK, (𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 4, 40), (0, 60), 4) pygame.draw.line(𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} , BLACK, (3 * 𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ} // 4, 40), (𝑐ℎ𝑎𝑟_{𝑤𝑖𝑑𝑡ℎ}, 60), 4)

𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑐ℎ𝑎𝑟𝑎𝑐𝑡𝑒𝑟} = pygame.transform.rotate(𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑠𝑢𝑟𝑓𝑎𝑐𝑒} , angle)
𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑟𝑒𝑐𝑡} = 𝑟𝑜𝑡𝑎𝑡𝑒𝑑_{𝑐ℎ𝑎𝑟𝑎𝑐𝑡𝑒𝑟.𝑔𝑒𝑡𝑟𝑒𝑐𝑡}(center=(𝑐ℎ𝑎𝑟_𝑥, 𝑐ℎ𝑎𝑟_𝑦)) screen.blit(_{𝑟𝑜𝑡𝑎𝑡𝑒𝑑𝑐ℎ𝑎𝑟𝑎𝑐𝑡𝑒, 𝑟𝑜𝑡𝑎𝑡𝑒𝑑𝑟𝑒𝑐𝑡.𝑡𝑜𝑝𝑙𝑒 𝑓 𝑡} )

pygame.draw.rect(screen, BLACK, (0, 𝑓𝑙𝑜𝑜𝑟_𝑦, WIDTH, HEIGHT – 𝑓𝑙𝑜𝑜𝑟_𝑦))

pygame.display.update()

frame = pygame.surfarray.array3d(screen)
frames.append(frame)

if len(frames) > 30:
running = False

clock.tick(20)

pygame.quit()

frames = [np.rot90(np.fliplr(frame)) for frame in frames] 𝑔𝑖𝑓_{𝑝𝑎𝑡ℎ} = ” 𝑓𝑎𝑙𝑙_{𝑠𝑖𝑚𝑢𝑙𝑎𝑡𝑖𝑜𝑛ℎ𝑢𝑚𝑎𝑛.𝑔𝑖𝑓} “
imageio.mimsave(𝑔𝑖𝑓_{𝑝𝑎𝑡ℎ}, frames, fps=10)
print(“GIF compile completed : 𝑓𝑎𝑙𝑙_{𝑠𝑖𝑚𝑢𝑙𝑎𝑡𝑖𝑜𝑛ℎ𝑢𝑚𝑎𝑛.𝑔𝑖𝑓} “)

2.6. Code Description

This section describes the code that simulates a person falling under gravity using Pygame. The simulation screen is shown in Figure 6. The figure is composed of basic shapes: a blue circle for the head, a red rectangle for the body, and black lines for the arms and legs. The figure starts falling from approximately 1.5 meters above the ground, using a scale of 50 pixels per meter to convert real-world measurements into the simulation. This scaling ensures that the motion of the figure appears realistic on the screen.

The code begins by setting up the display and defining key physics variables such as gravity, time step, velocity, and position. Based on these calculations, each frame determines the falling speed of the figure and updates its position accordingly. If the rotational fall option is enabled, the figure rotates by 5 degrees per frame to simulate how people naturally rotate during a fall. This addition makes the fall appear more realistic compared to a simple straight drop.

The simulation continues running until the figure reaches the floor. At that point, the program stops the falling motion by resetting the velocity to zero and ceasing the rotation. This approach ensures that the figure does not pass through the floor, replicating a realistic landing behavior.

One important feature of the code is the capture of every simulation frame, which is saved as a list. After 30 frames, these images are processed and saved as a GIF file named fall_simulation_human.gif. This feature allows the entire falling motion to be easily reviewed and analyzed later. Observing the GIF makes it more convenient to analyze how variables like rotation speed, fall duration, and gravity influence the fall dynamics.

In general, the code was designed to visualize a person’s fall under gravity, incorporating both vertical and rotational movements. The GIF-saving feature is particularly useful because it allows the complete fall sequence to be observed from start to finish without having to rerun the simulation repeatedly. This helps in analyzing how different factors affect human falls and improves the understanding of the physics involved.

Figure 7 and Figure 8 provide a detailed view of the code structure and implementation. These figures show the primary components and the logical flow of the simulation.

3. Advantages and Significance of This Paper

3.1. An Accurate Analysis of Complex Phenomena in the Real World

Human movements are highly complex and involve various physical elements such as force, torque, and acceleration. Based on physical theory, these complex behaviors can be systematically described using mathematical equations. For example, in the case of a fall, physical principles such as momentum, impact force, and rotational motion can be utilized to analyze the underlying mechanisms. This accurate analysis aids in understanding the dynamics of falls and helps develop effective prevention strategies.

3.2. Safe and Efficient Replacement of Experiments

Conducting experiments directly with people can be dangerous or unethical, especially when studying falls among seniors. It is not feasible to deliberately induce falls for re- search purposes. Instead, computer simulations implement physical theories as code to replicate real-world scenarios, allowing experiments to be conducted safely. These simulations enable the analysis of fall dynamics without putting individuals at risk, providing an efficient and ethical alternative to direct experimentation.

4. Further Research

Understanding the distribution of impact forces in different types of falls provides valuable insights into injury prevention. Future research should focus on practical applications of impact force reduction techniques.

One key area of study is extending the duration of the impact. Since the impact force is inversely proportional to the impact time, as shown in Equation 13:

$$I = \frac{m\sqrt{2gh}}{t} \tag{13}$$

Increasing the impact duration can significantly reduce the risk of injury. To achieve this, researchers are investigating smart flooring materials that absorb energy and extend collision time. Additionally, advanced hip protectors are being developed to distribute the impact over a larger surface area, minimizing the chances of fractures.

Another promising area of research is the development of AI-based fall detection and prevention systems. Machine learning models can predict the risk of falling in elderly individuals by analyzing motion patterns, while wearable devices equipped with gyroscopes and accelerometers detect early signs of imbalance. These systems can be integrated with protective mechanisms, such as airbags, that deploy before impact to minimize injuries.

In addition, personalized fall risk assessment is an emerging field that leverages biomechanical simulations and clinical trials to validate injury models. Data from motion capture studies and sensor-based fall monitoring help tailor protective measures to individual risk factors, ultimately enhancing fall prevention strategies.

By integrating engineering solutions with medical research, future studies can contribute to more effective injury prevention technologies, ultimately improving the safety and quality of life of seniors.

5. Conclusion

In an aging society, elderly falls are a serious social and economic problem, and preventing them is important to improve the quality of life of individuals and reduce social costs. This study used physical concepts such as momentum, angular momentum, and impact force to analyze falls. We looked at the physical mechanisms involved by dividing falls into straight and rotational types. We rechecked the results of the physical analysis using a Pygame simulation and confirmed how different factors, such as weight and collision time, affect falls. This study aims to help improve the safety and health of seniors by understanding how falls occur from a scientific perspective and finding ways to prevent them. In the future, we hope this research can lead to practical solutions, such as developing protective equipment, creating AI-based systems to predict falls, and promoting exercise programs to prevent falls so seniors can live more safely and healthily.

1. S.-Y. Cheng, C.-P. Lin, H. Y.-l. Chan, D. Martina, M. Mori, S.-H. Kim, R. Ng, “Advance care planning in asian culture”, Japanese Journal of Clinical Oncology, vol. 50, no. 9, pp. 976 989, 2020, doi:10.1093/jjco/hyaa131.
2. D. Gu, K. Andreev, M. E. Dupre, “Major trends in population growth around the world”, China CDC Weekly, vol. 3, no. 28, pp. 604–613, 2021, doi:10.46234/ccdcw2021.160.
3. K. Peng, M. Tian, M. Andersen, J. Zhang, Y. Liu, Q. Wang, R. Lindley, R. Ivers, “Incidence, risk factors and economic burden of fall-related injuries in older chinese people: a systematic review”, Injury Prevention, vol. 25, no. 1, pp. 4–12, 2019, doi:10.1136/injuryprev-2018 042982.
4. R.Vaishya,A.Vaish, “Falls in older adults are serious”, Indian Journal of Orthopaedics, vol. 54, pp. 69–74, 2020, doi:10.1007/s43465-019-00011-w.
5. G. . A. Collaborators, “Global, regional, and national burden of diseases and injuries for adults 70 years and older: systematic analysis for the global burden of disease 2019 study”, BMJ, vol. 376, 2022, doi:10.1136/bmj-2021-068208.
6. S. A. Boamah, R. Weldrick, T.-S. J. Lee, N. Taylor, “Social isolation among older adults in long-term care: a scoping review”, Journal of Aging and Health, vol. 33, no. 7-8, pp. 618–632, 2021, doi:10.1177/08982643211004138.
7. C. S. Florence, G. Bergen, A. Atherly, E. Burns, J. Stevens, C. Drake, “Medical costs of fatal and nonfatal falls in older adults”, Journal of the American Geriatrics Society, vol. 66, no. 4, pp. 693–698, 2018, doi:10.1111/jgs.15304.
8. L. Ren, Y. Peng, “Research of fall detection and fall prevention technologies: A systematic review”, IEEE Access, vol. 7, pp. 77702–77722, 2019, doi:10.1109/ACCESS.2019.292270.
9. T. Xu, Y. Zhou, J. Zhu, “New advances and challenges of fall detection systems: A survey”, Applied Sciences, vol. 8, no. 3, p. 418, 2018, doi:10.3390/app8030418.
10. J. M. Guirguis-Blake, Y. L. Michael, L. A. Perdue, E. L. Coppola, T. L. Beil, “Interventions to prevent falls in older adults: updated evidence report and systematic review for the us preventive services task force”, Jama, vol. 319, no. 16, pp. 1705–1716, 2018, doi:10.1001/jama.2017.21962.
11. M. Montero-Odasso, N. Van Der Velde, F. C. Martin, M. Petrovic, M. P. Tan, J. Ryg, S. Aguilar-Navarro, N. B. Alexander, C. Becker, H. Blain, et al., “World guidelines for falls prevention and management for older adults: a global initiative”, Age and ageing, vol. 51, no. 9, p. afac205, 2022, doi:10.1093/ageing/afac205.
12. E. Rudnicka, P. Napierała, A. Podfigurna, B. Męczekalski, R. Smolarczyk, M. Grymowicz, “The world health organization (who) approach to healthy ageing”, Maturitas, vol. 139, pp. 6–11, 2020, doi:10.1016/j.maturitas.2020.05.018.
13. M. Ronthal, “Gait disorders and falls in the elderly”, Medical Clinics, vol. 103, no. 2, pp. 203–213, 2019, doi:10.1016/j.mcna.2018.08.005.
14. T. Kim, S. D. Choi, S. Xiong, “Epidemiology of fall and its socioeconomic risk factors in community-dwelling korean elderly”, PloS one, vol. 15, no. 6, p. e0234787, 2020, doi:10.1371/journal.pone.0234787.

Citations by Dimensions

Citations by PlumX

Crossref Citations

No related articles were found.